DC est un diamètre du cercle. Démontrer que le triangle DBC est rectangle en B.
Pythagore et le cercle
Catégorie : Exercices
Cercle et rayon
ABCD est un carré de côté 4. Le triangle ABC est rectangle isocèle en B, AC est son hypoténuse.
AB = BC = 4
D’après Pythagore on a:
AC² = AB² + BC² = 4² + 4² = 32
AC = \sqrt{32} = 4 \sqrt{2} Cercle et rayon
On a un cercle de rayon 4 et de centre C.
Que vaut la longueur de AC ?
Exercices
Sablier
Sablier
Le four à micro-ondes
Le plat est plus petit (L=27 cm et P=18 cm) que la taille intérieure du micro-ondes (L=40 cm et P=30 cm), donc il peut entrer dedans.
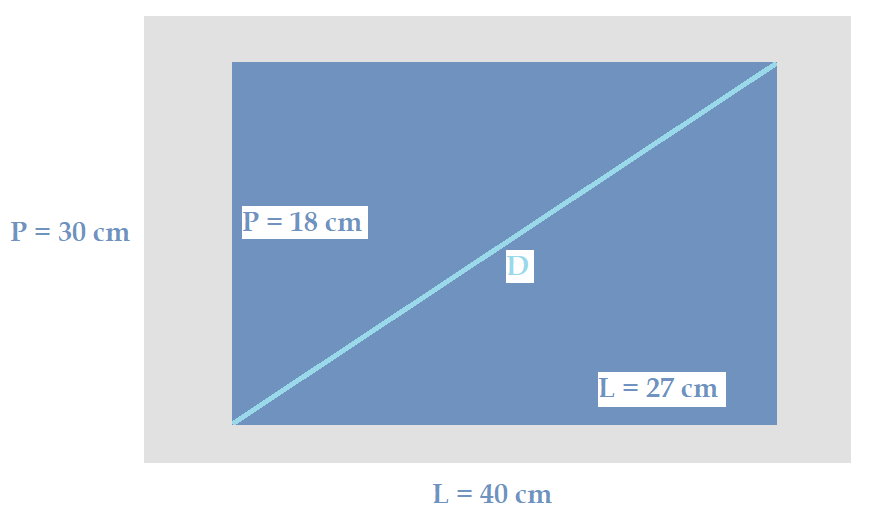
Maintenant que nous savons que le plat entre dans le micro-ondes, il reste à voir s’il peut tourner… ???
\textrm{Le plat peut tourner si la diagonale} \\
\textrm{du plat D n'excède pas 30 cm.} \\[0.15int]
\textrm{On calcule:} \\[0.15int]
\textrm{D² = }\mathrm{18^2+27^2} \\[0.15int]
\mathrm{D^2=1053} \\[0.15int]
\mathrm{D = \sqrt{1053}\approx{32,4 cm}} \\[0.3int]
\textrm{Donc le plat ne peut pas tourner.}Échelle
Ici, on utilise un cosinus. Le côté adjacent est égal à la hauteur du mur (BH). L’hypoténuse est égal à la longueur de l’échelle (AB).
D’après l’énoncé, la hauteur maximale est atteinte lorsque l’on a un angle de 30°.
\textrm{AB = 5 m} \\ [0.15int]
\mathrm{cos ~30°= \frac{BH}{5}} \\ [0.15int]
\mathrm{D'où:BH = 5~cos~30°} \\ [0.15int]
\textrm{BH = 4,33 m}D’après l’énoncé, la hauteur minimale est atteinte lorsque l’on a un angle de 45°.
\textrm{AB = 5 m} \\ [0.15int]
\mathrm{cos ~45°= \frac{BH}{5}} \\ [0.15int]
\mathrm{D'où:BH = 5~cos~45°} \\ [0.15int]
\textrm{BH = 3,54 m}Conclusion :
Pour travailler en sécurité, on peut utiliser l’échelle pour atteindre un toiture comprise entre 3,54 m et 4,33 m.
Échelle
Un couvreur veut acheter une échelle de 5m pour atteindre une toiture. Dans le catalogue d’un de ses fournisseurs, il en trouve une à 200 € HT.
La notice de cette échelle préconise une inclinaison par rapport au mur de 30° à 45° pour un usage en toute sécurité.
Quelle hauteur maximale et minimale l’échelle peut-elle atteindre en respectant la notice ?
Arrondir le résultat au centimètre. On suppose que le mur est perpendiculaire au sol.
N.B. : Les valeurs « de sécurité » utilisées dans cet exercice sont purement imaginées et n’engagent en rien les fabricants. Il est préférable de se référer au mode d’emploi fourni par le fabricant en utilisation réelle.
Phare
La figure n’est pas à l’échelle.
\textrm{A : Position du bateau le soir} \\
\textrm{B : Position du bateau le lendemain matin} \\[0.3int]
\underline{\textrm{Le triangle AOS est rectangle en O :}} \\[0.05int]
\textrm{tan 45° = 1, donc OA = OS = 40 m.} \\[0.3int]
\underline{\textrm{Le triangle BOS est rectangle en O :}} \\[0.05int]
\mathrm{tan~ 60°= \frac{OS}{OB}= \frac{40}{OB}} \\[0.15int]
\mathrm{OB= \frac{40}{tan~60°}} \\[0.15int]
\mathrm{OB \approx 23,1~m} \\[0.3int]
\underline{\textrm{AB est la distance de déplacement du bateau,}} \\
\underline{\textrm{entre le soir et le matin, on en déduit que :}} \\[0.05int]
\mathrm{AB = AO-BO = 40-23,1} \\[0.05int]
\mathrm{AB \approx 16,9~m} \\[0.3int]
\textrm{Le bateau s'est rapproché de 16,9 m environ.} \\
\textrm{16,9 < 25 , \textbf{le bateau doit donc être déplacé.}}