Pythagore
Auteur/autrice : Romain
Pi, cercle et trigonométrie
Retour en maternelle! ^^
Enoncé:
Correction:
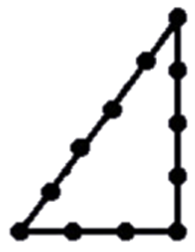
On commence par la première ligne: le « triangle » vaut 2, car 2^3 x 3 = 24.
Dans la deuxième ligne, le « disque » vaut 4, car 3 x 2 x 4² = 96.
Donc: 4 + 3 x 2 = 10.
1peu2tout… pour s’entraîner!
Le cercle trigonométrique
Définition
Le cercle trigonométrique est un cercle de rayon 1.
Sur l’axe des abscisses on a les cosinus.
Sur l’axe des ordonnées on a les sinus.
Le cercle trigonométrique permet de représenter le sinus, le cosinus et la tangente d’un angle θ.
Propriétés
sin²θ + cos²θ = 1 (Pythagore)
-1⩽ sinθ ⩽1 et -1⩽ cosθ ⩽1
Quelques valeurs de référence…
Les ammonites…
Les ammonites sont un type de mollusque marin préhistorique. Ils ont vécu pendant plus de 300 millions d’années, de la période dévonienne à la fin du crétacé. Ils ont disparu à la même époque que les dinosaures.
Le nombre d’or: 1.61803…
L’enroulement régulier d’une ammonite se fait suivant une spirale logarithmique, la spirale d’or, comme de nombreux coquillages qui sont formés ainsi.
L’étoile de mer est un pentagone régulier étoilé, qui est en relation direct avec le nombre d’or.
La fleur de vie
La fleur de vie est une figure géométrique constituée de plusieurs cercles identiques qui s’entrecroisent et se relient centre-à-centre.. Cette figure géométriques regroupe le nombre d’or et la suite de Fibonacci.
La figure est constituée d’au moins sept cercles. Six cercles environnants se croisent au centre d’un septième cercle. Cependant, les cercles environnants ne sont pas forcément dessinés entièrement. La fleur de vie forme un modèle hexagonale symétrique.
On retrouve le nombre d’or dans toutes les dimensions de la fleur de vie.
Un point d’histoire
La Fleur de Vie se retrouve dans de nombreuses cultures et religions. Elle a été retrouvée en Égypte, Israël, au Mont Sinaï, en Inde, en Europe et dans de nombreux temples Japonais et Chinois.
En Assyrie, on peut voir exemple de modèle répétitif construit comme la fleur de vie. Cette construction en albâtre date de 645 av. J.-C.
A Abydos en Égypte, on peut voir des gravures ressemblant à la fleur de vie sur des colonnes de granit du temple d’Osiris. Certaines d’entre elles sont difficiles à distinguer à cause de l’érosion.
Dans le Codex Atlanticus rédigé par Leonard de Vinci entre 1478 et 1519 il y a quelques figures ressemblants à la « fleur de vie ».
Le logo du parc naturel du Queyras (France) contient une rosette du centre de la « fleur de vie ».
La fleur de vie est un motif décoratif depuis des temps immémoriaux.
La fleur de vie à la base de la vie
L’œuf de vie est composé de 7 cercles extraits de la fleur de vie. Il représente un embryon dans ses premières heures de formation.
Pi et le cercle
π (Pi) ou constante d’Archimède est est un nombre représenté par la lettre grecque du même nom.
Définition
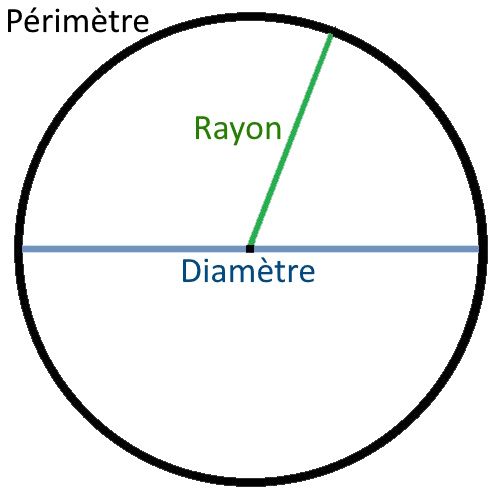
π est le rapport constant entre le périmètre (P) du cercle et son diamètre (D). D’où: π=P/D. Il y a proportionnalité entre le périmètre et le diamètre.
π est le rapport constant entre l’aire (A) d’un disque et son rayon au carré (R²). D’où: π=A/R². Il y a proportionnalité entre l’aire et le rayon au carré.
Représentation du rapport entre le périmètre et le diamètre
Position de départ
Position après un tour de roue
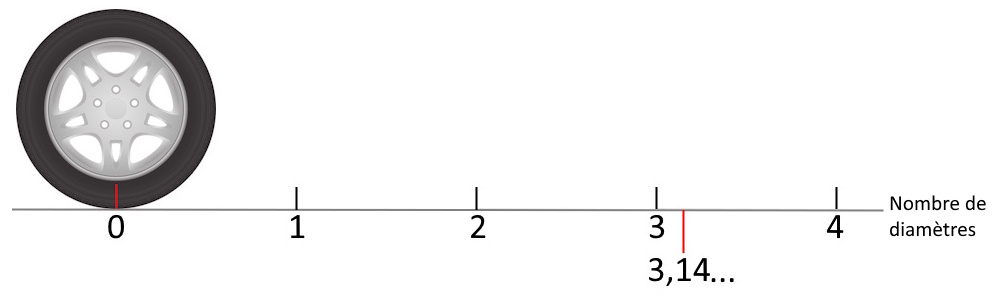
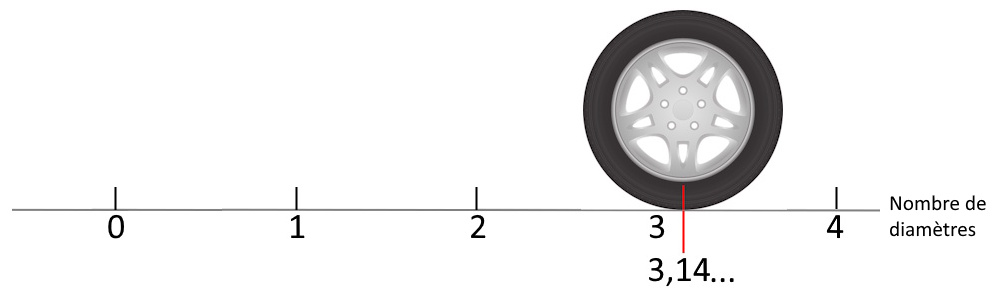
Périmètre = Pi x diamètre
Écrit autrement on retrouve: P = πD = 2πR
Pi, un nombre sans fin!
Le nombre Pi suscite un intérêt chez les mathématiciens depuis près de 4000 ans.
Très tôt les mathématiciens soupçonnent l’existence d’une constante entre le périmètre d’un cercle et son diamètre. Vers 2000 ans av. J.-C., on retrouve des traces de Pi chez les babyloniens et les égyptiens. Vers 700 av. J.-C., un texte indien fournit une approximation de Pi à 3,125. Vers 250 av. J.-C., Archimède (287-212 av. J.-C.) apporta une bonne approximation du nombre pi en utilisant une méthode d’encadrement.
Archimède et Pi
Archimède encadra un cercle par son polygone inscrit et son polygone circonscrit. Cette méthode est appelée l’exhaustion, c’est une méthode ancienne qui devient vite lourde à mesure que l’on augmente le nombre de côtés des polygones. Avec cette méthode, on peut encadrer le périmètre d’un cercle mais aussi l’aire d’un disque. Dans les deux cas, on peut mettre en avant une approximation du nombre Pi.
En utilisant un polygone à 96 côtés, Archimède parvient à une bonne approximation : 223/71≤π≤22/7.
Les recherches continuent…
Au fil des siècles, les méthodes pour calculer les décimales de Pi se poursuivent: en Chine au IIIe siècle, puis en Inde vers le XVe siècle.
La notation π (16e lettre de l’alphabet grec) n’apparait qu’en 1647. Inspirée d’Archimède qui désignait la longueur de la circonférence par le mot «περιμετροε» (périmètre), et de l’anglais William Oughtred (1574-1660) qui l’utilisa pour nommer le périmètre d’un cercle.
A la fin du XVIe siècle, le français Adrien Romain arrive à calculer 15 décimales de Pi. Il fut supplanté au début du XVIIe siècle par l’allemand Ludolph van Ceulen qui calcula 35 décimales.
Les machines à la rescousse…
Le 14 mars 2019, jour du Pi-Day, Google rend public le nouveau record de calcul des décimales de Pi: 31 415 milliards de décimales.
Le 28 juin 2024, un nouveau record de calcul des décimales de Pi a été établi, avec plus de 202 mille milliards de décimales.
La première contribution décisive intervient cependant en Europe, grâce au mathématicien français François Viète (1540-1603), qui parvient à calculer 12 décimales.
La corde à 13 nœuds
La corde peut servir à:
– prendre et reporter des mesures,
– tracer des cercles et des arcs de cercle,
– fabriquer des formes géométriques (triangle rectangle, isocèle ou équilatéral),
– fabriquer des angles droits.
Le triplet (3, 4, 5) est bien connu pour former un triangle rectangle.
Pour l’époque, cet outil était pratique pour vérifier l’équerrage des parcelles de terre. En effet, transporter un rouleau de corde est plus facile que de transporter une équerre géante.
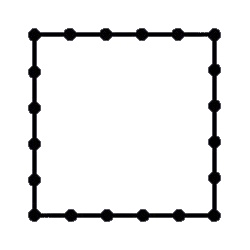
Il existe plusieurs types de corde. La corde à 20 nœuds permet de construire un carré et plusieurs rectangles.
La corde à treize nœuds ou « corde des druides » ou « corde égyptienne » est une corde avec treize nœuds espacés de façon régulière. Fabriquer une de ces cordes n’est pas si facile!
Son origine est mal connue. On retrouve des traces de son utilisation chez les architectes de l’Egypte antique, pour tracer des angles droits. Elle fut aussi utilisée par les bâtisseurs du Moyen âge.
A cette époque, très peu de personnes avaient des notions de calcul ou de géométrie. De plus, les systèmes de mesures utilisés étaient aussi diverses que variés, ce qui ne facilitait rien!
